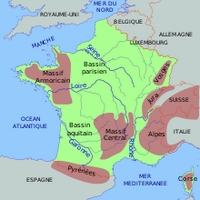
Ci-dessous la carte de France inscrite dans un rectangle. Nous lançons des points de manière aléatoire dans le rectangle. Les points tombent ou ne tombent à l’intérieur des frontières françaises. En rapportant le nombre de points à l’intérieur au nombre total de points tirés nous construisons ainsi un estimateur de la surface de ce pays. Il suffit pour cela de multiplier le rapport ainsi obtenu par la surface (connue) du rectangle. Nous nous approchons sensiblement de la valeur réelle de cette surface (643801 km²). Pour ouvrir le projet dans une autre fenêtre cliquer ici.
Ci-dessous, deux lettres M et K, inscrites dans un carré découpé en 4 parties égales. Les deux lettres apparaissent successivement de manière aléatoire. Nous lançons des points au hasard dans le carré. Ils nous permettent d’estimer la surface couverte par la lettre dans chaque partie du carré. Nous construisons à partir de ces valeurs deux indicateurs : le premier évalue la différence horizontale de surface occupée par la lettre tandis que le deuxième évalue la différence verticale de surface occupée par la lettre. Clairement lorsque le premier est supérieur au second, il s’agit de la lettre M, tandis que dans le cas contraire il s’agit de la lettre K. Nous pouvons vérifier, en répétant l’opération plusieurs fois, que notre algorithme ne se trompe pas. Pour ouvrir le projet dans une autre fenêtre cliquer ici.
Ci-dessous, deux quarts de cercles de rayon 1 inscrits dans deux carrés de côtés 1. Nous retrouvons notre estimateur de Pi initial évalué par 4 fois le rapport entre les points dans le quart de disque et le nombre total de points tirés. Cet estimateur, pour un nombre total de points lancés fixé (100), fluctue autour de la valeur exacte de Pi. Un indicateur, la variance, mesure ces fluctuations. Une problématique importante dans le cadre de la méthode de Monte-Carlo est celle de la réduction de la variance. Une variance réduite, assure des fluctuations de l’estimateur moins importantes et permet de programmer des algorithmes plus efficaces. Pour réduire la variance, il existe plusieurs méthodes. Nous nous intéressons ici à l’utilisation des variables antithétiques. Dans le carré du haut, nous tirons 100 séries de 100 points pris complètement au hasard (c’est à dire indépendants les uns des autres). Dans le carré du bas nous tirons 100 séries de 100 points pour lesquels, les 50 premiers sont identiques aux 50 premiers du carré du haut et les 50 suivants sont liés aux 50 premiers par la relation suivante : x devient 1-x et y devient 1-y. Nous créons ainsi une dépendance entre les points et observons, dans la plupart des cas, une réduction de la variance. Pour ouvrir le projet dans une autre fenêtre cliquer ici.