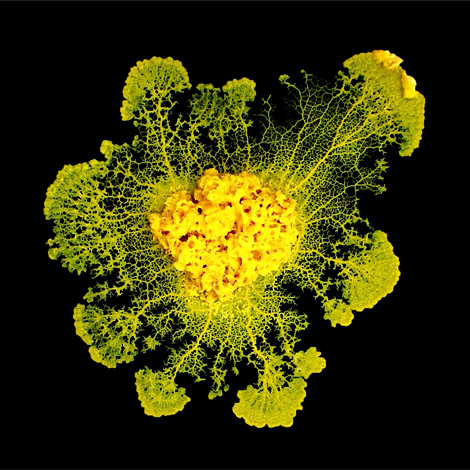
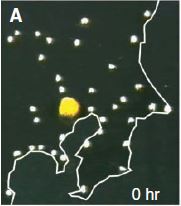
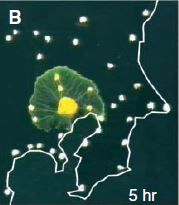
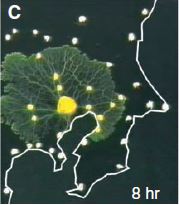
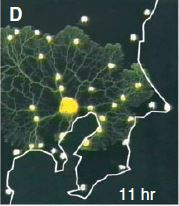
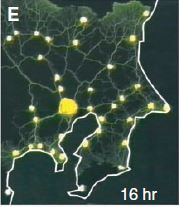
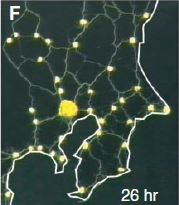
Le blob (physarum polycephalum) est un être étrange. Entre animal, végétal et champignon. Unicellulaire, il s’étend pour couvrir une surface maximale, puis se concentre et fond pour ne garder que les axes les plus utiles pour faire circuler la nourriture dans son corps. Des chercheurs japonais ont étudié plus précisément ce mode de déplacement et ont conclu qu’il constituait une méthode d’optimisation spatiale très performante, proche d’autres structures de réseaux optimisés comme le métro de Tokyo.
Comment optimiser la distance d’un réseau reliant trois points ? Comment optimiser la distance d’un réseau reliant quatre points ? Voilà deux questions mathématiques que nous allons nous poser au cours de cet exposé pour essayer de comprendre ce que fait le blob. Et pour commencer, étant donné que nous sommes très curieux, ce sont des questions que nous allons VOUS poser pour essayer de comprendre ce que vous savez des maths ! Etant donné quatre points, sommets d’un rectangle, comment optimiser la distance d’un réseau les reliant ? Nous vous aidons un peu en vous proposant 4 réponses types : « un réseau en forme de H », « un réseau en forme de X », « un réseau d’une autre forme encore à définir », « sans réponse car le blob vous effraie »…
Tous à vos téléphones portables ! Vous pouvez soit flasher le QR code, soit utiliser l’adresse raccourcie pour accéder à notre questionnaire. Nous sommes très curieux de connaître vos réponses… Alors à vos maths, prêts ? Votez !
Pour accéder au questionnaire : http://urlz.fr/6GZA |
Pour accéder aux réponses : http://urlz.fr/6GZU |
Comment optimiser la distance d’un réseau reliant trois points ? Comment optimiser la distance d’un réseau reliant quatre points ? Plus sérieusement, pour répondre à ces deux questions, nous ferons désormais appel à un matériau qui a tendance à minimiser sa surface : un peu d’eau savonneuse emprisonnée entre deux plaques de plexiglas parallèles fera l’affaire. Pour répondre à la première nous utiliserons trois vis. Pour répondre à la seconde nous en ajouterons une.
Comment faire sans eau savonneuse ? Faisons appel à la programmation. Tirons au hasard un point à l’intérieur d’un triangle (ou d’un rectangle), calculons la taille du réseau reliant les trois sommets (ou les quatre), colorons différemment chaque point en fonction de la taille obtenue afin de localiser celui (ou ceux) qui minimise(nt) la distance. Observez attentivement le résultat !
En manque de temps ? La flemme d’attendre ? Il est vrai que dans le triangle nous tirons au hasard 500000 points. Il est également vrai que dans le rectangle nous tirons au hasard 400000 points, ce qui, pour des raisons de symétrie, revient à en tirer 100000. Tout cela prend du temps. En cliquant sur les liens ci-dessus, vous pourrez regarder, si le cœur vous en dit, le code de l’algorithme et activer le mode turbo. Si c’est l’aspect esthétique qui vous fascine, deux films accélèrent les choses et vous permettent de profiter pleinement du spectacle !