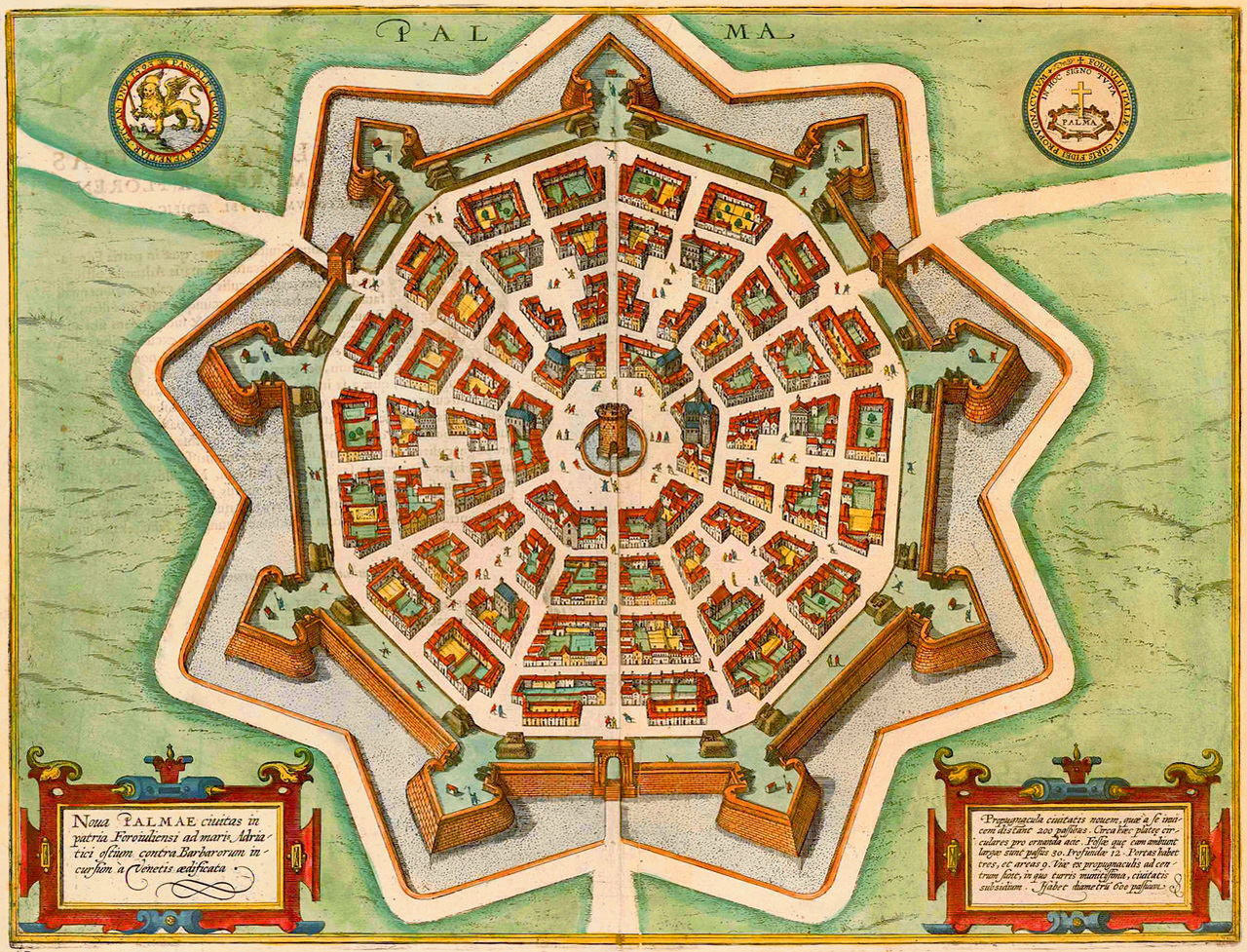
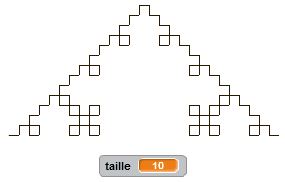
Palmanova est une commune italienne située dans la province d’Udine, dans la région autonome du Frioul-Vénétie julienne, dans le nord-est de l’Italie. La commune est célèbre pour sa forteresse en forme d’étoile à 9 branches, conçue par Vincenzo Scamozzi. Entre les pointes de l’étoile, des bastions permettent à chaque pointe de défendre ses voisines. Un fossé entoure la ville, et trois grandes portes gardées en contrôlent les entrées. Nous pensons immédiatement à un motif fractal célèbre : le flocon de Von Koch.
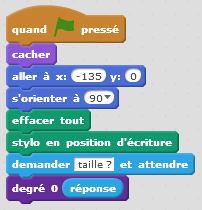
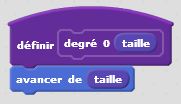
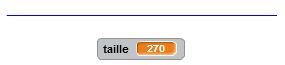
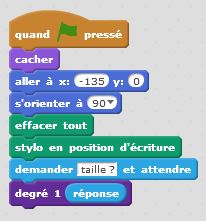
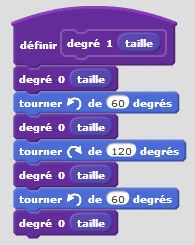
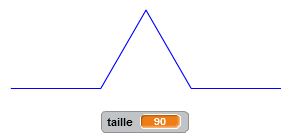
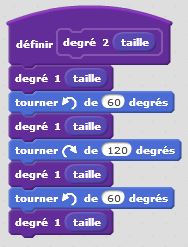
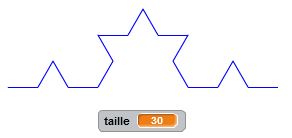
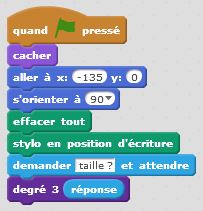
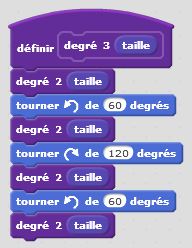
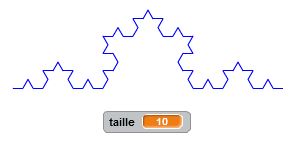
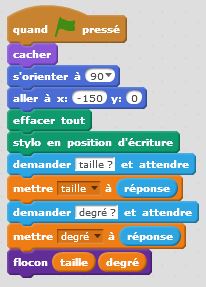
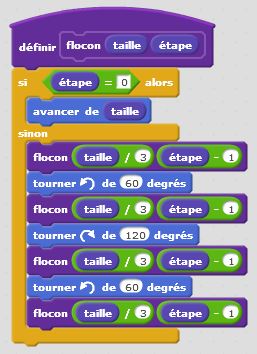
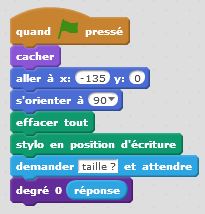
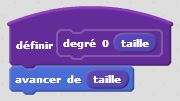
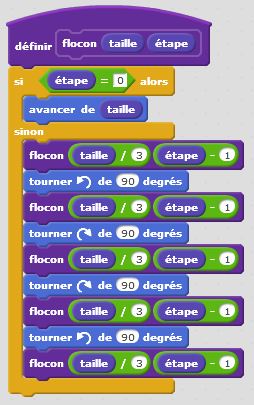
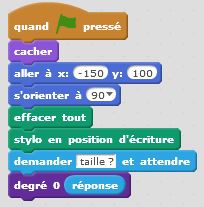
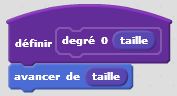
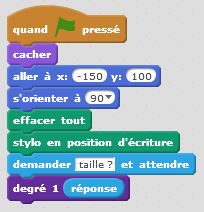
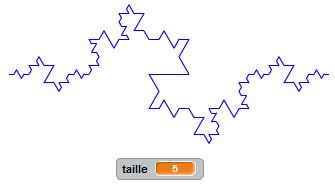
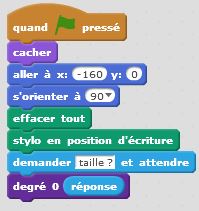
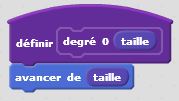
Degré 0 : j’avance. C’est un premier bloc d’instruction. Degré 1 : j’avance, je tourne de +60°, j’avance, je tourne de -120°, j’avance, je tourne de +60°, j’avance. C’est un deuxième bloc d’instruction dans lequel s’insère naturellement le premier bloc. Et ainsi de suite… Le principe de récursivité naît de cette logique. Un bloc d’instruction paramétré par la taille et l’étape fait intervenir lui-même à une taille inférieure et à une étape précédente. Cette idée simple, matérialisée dans nos algorithmes par une instruction conditionnelle du type « Si … Alors… Sinon… » permet de condenser les programmes et de tracer des motifs fractals d’une taille et d’un degré donnés. On utilise à plein le principe d’auto-similarité de ces motifs.
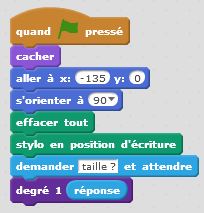
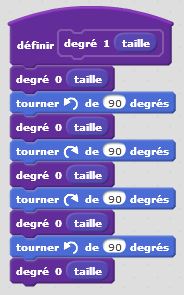
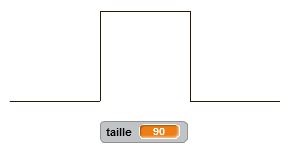
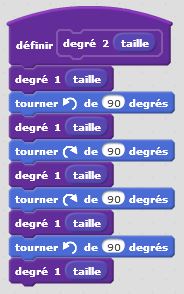
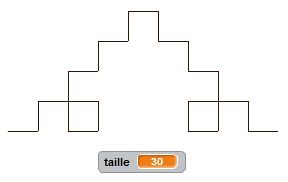
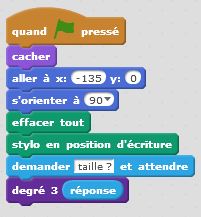
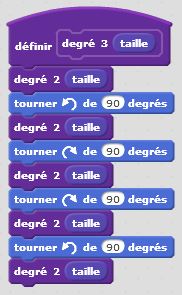
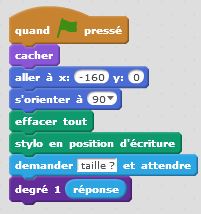
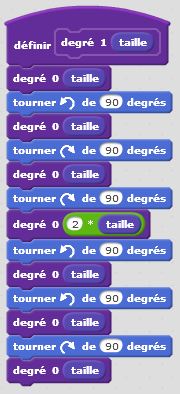
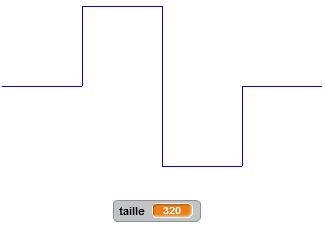
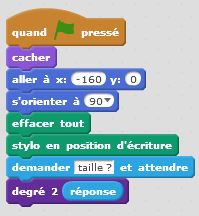
Degré 0 : j’avance. Degré 1 : j’avance, je tourne de +90°, j’avance, je tourne de -90°, j’avance, je tourne de -90°, j’avance, je tourne de +90°, j’avance. Et ainsi de suite… Nous décrivons ainsi, un autre motif fractal, similaire au premier. Il nous permet de tracer le carré de Von Koch. Là encore le principe de récursivité s’applique et nous permet de condenser nos programmes afin d’être en mesure de tracer le motif pour une taille et un degré donnés.
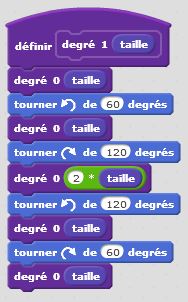
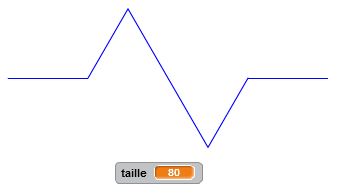
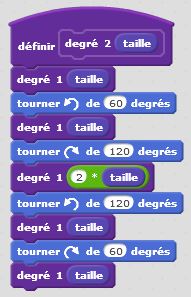
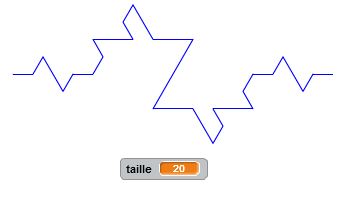
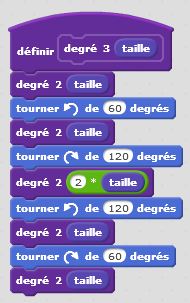
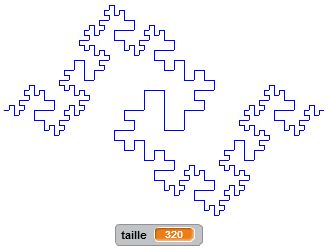
Degré 0 : j’avance. Degré 1 : j’avance, je tourne de +60°, j’avance, je tourne de -120°, j’avance du double de la longueur, je tourne de +120°, j’avance, je tourne de -60°, j’avance. Et ainsi de suite… Nous décrivons ici un autre motif fractal, qui, lorsque le degré devient grand, donne naissance à des formes géométriques intéressantes, complexes mais très ordonnées.
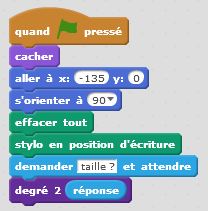
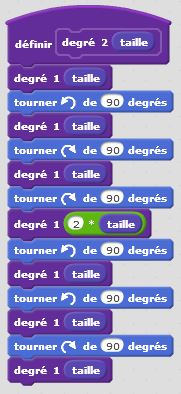
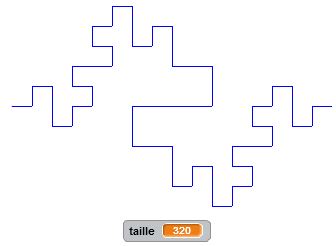
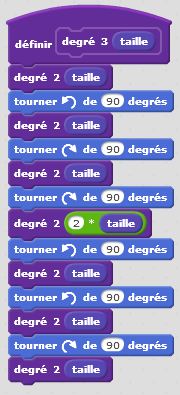
Degré 0 : j’avance. Degré 1 : j’avance, je tourne de +90°, j’avance, je tourne de -90°, j’avance, je tourne de -90°, j’avance du double de la longueur, je tourne de +90°, j’avance, je tourne de +90°, j’avance, je tourne de -90°, j’avance. Et ainsi de suite… Nous décrivons ici un autre motif fractal, qui, lorsque le degré devient grand, donne naissance à des formes géométriques intéressantes, complexes mais très ordonnées.