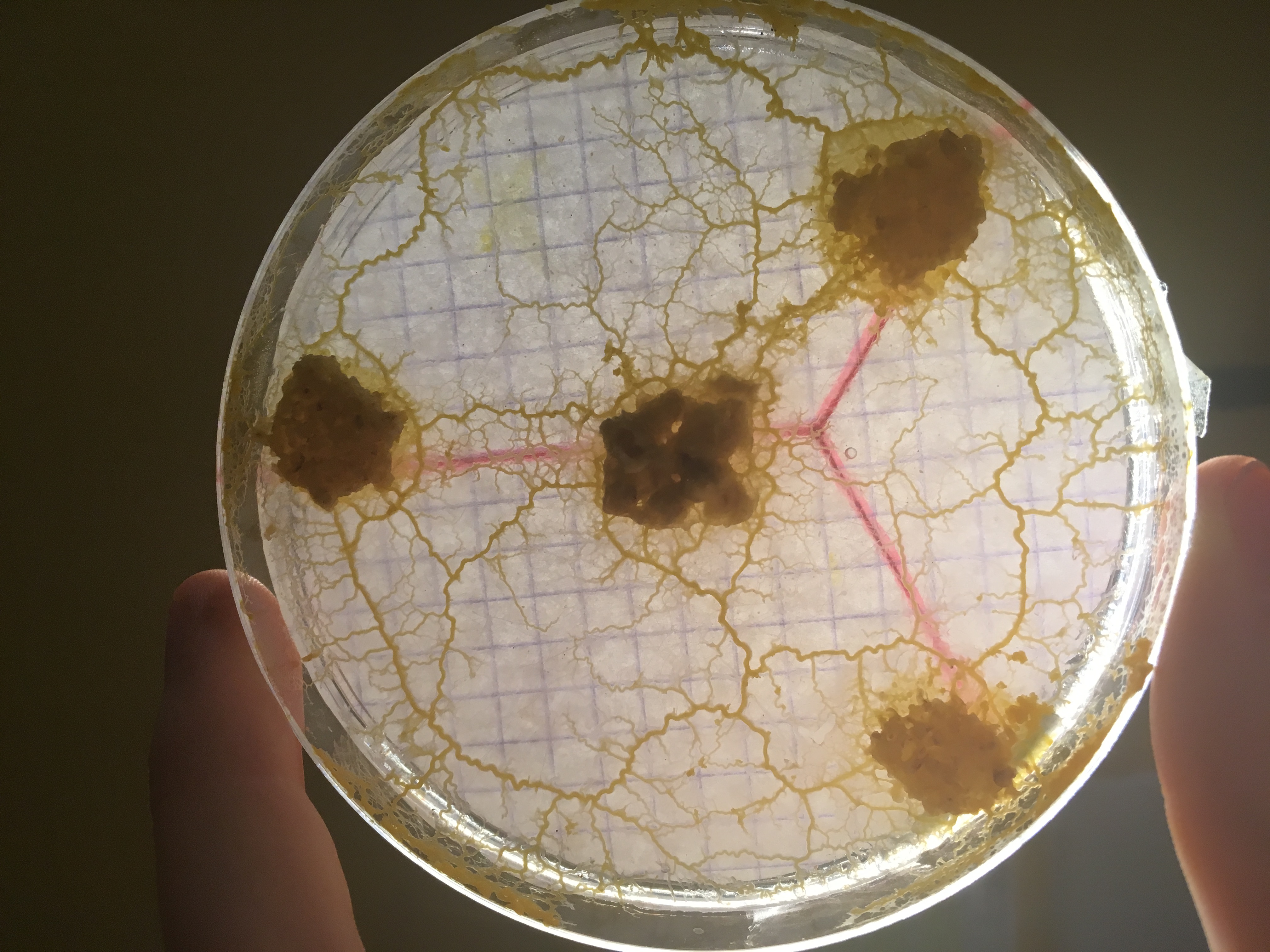
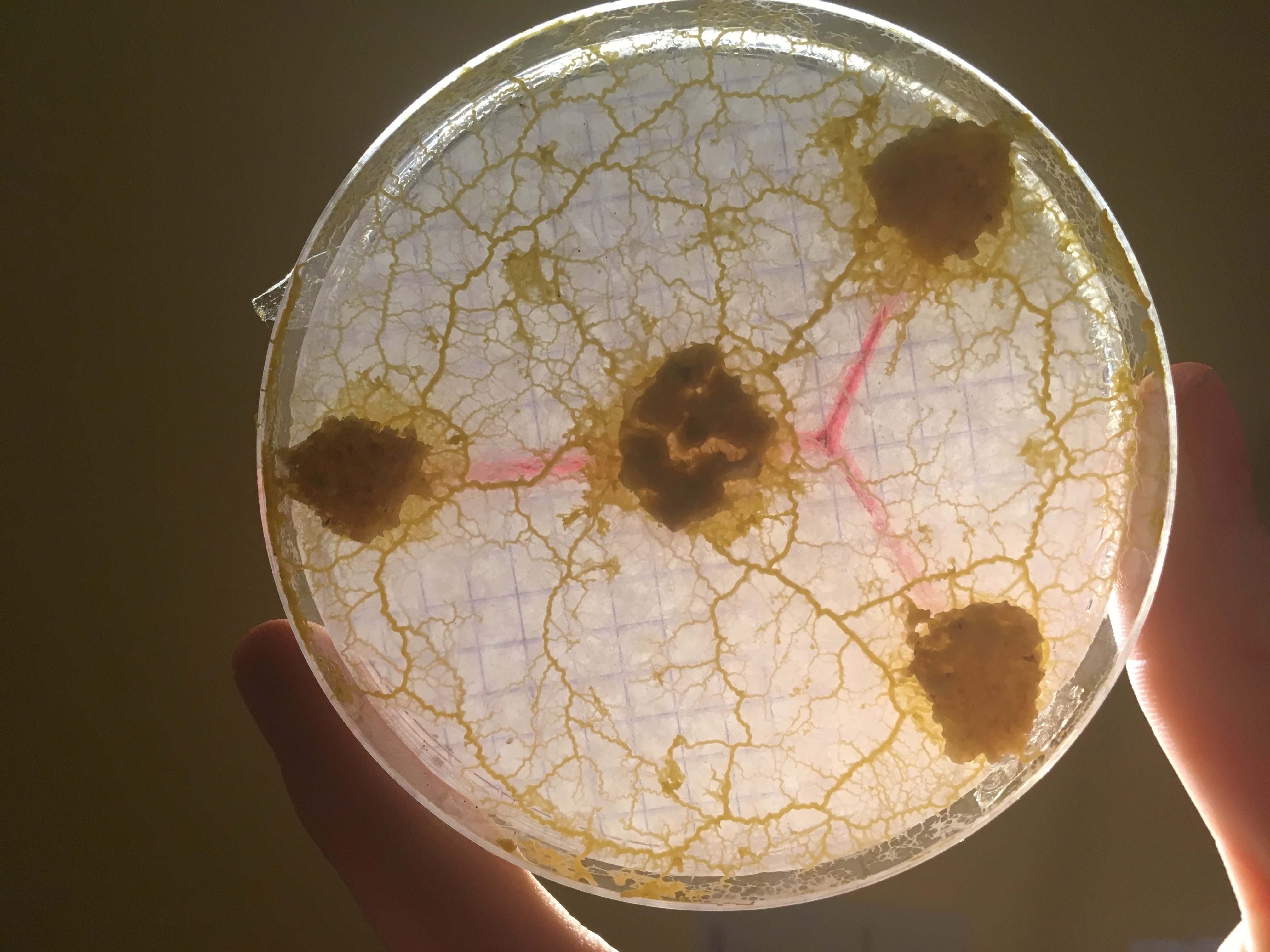
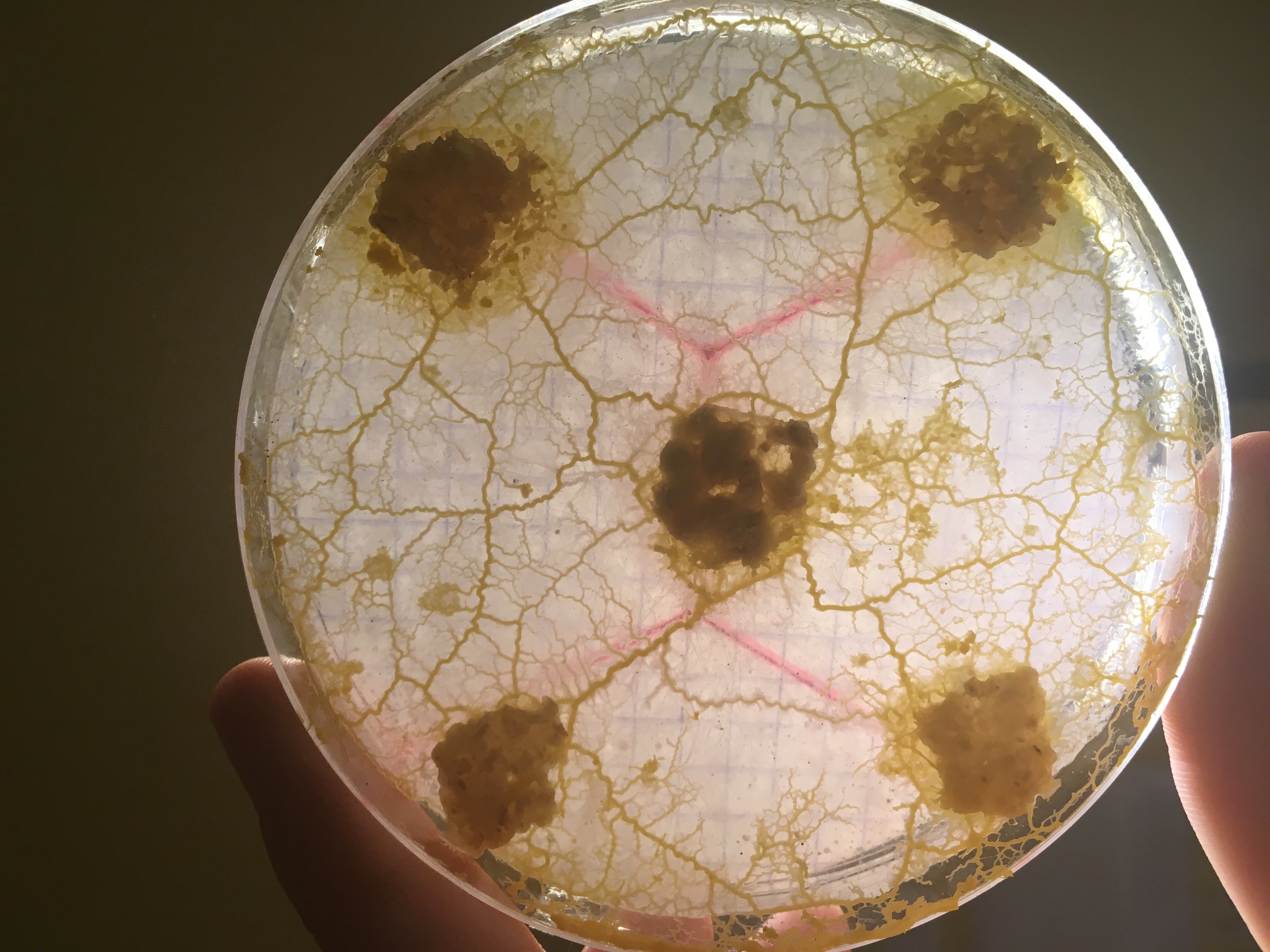
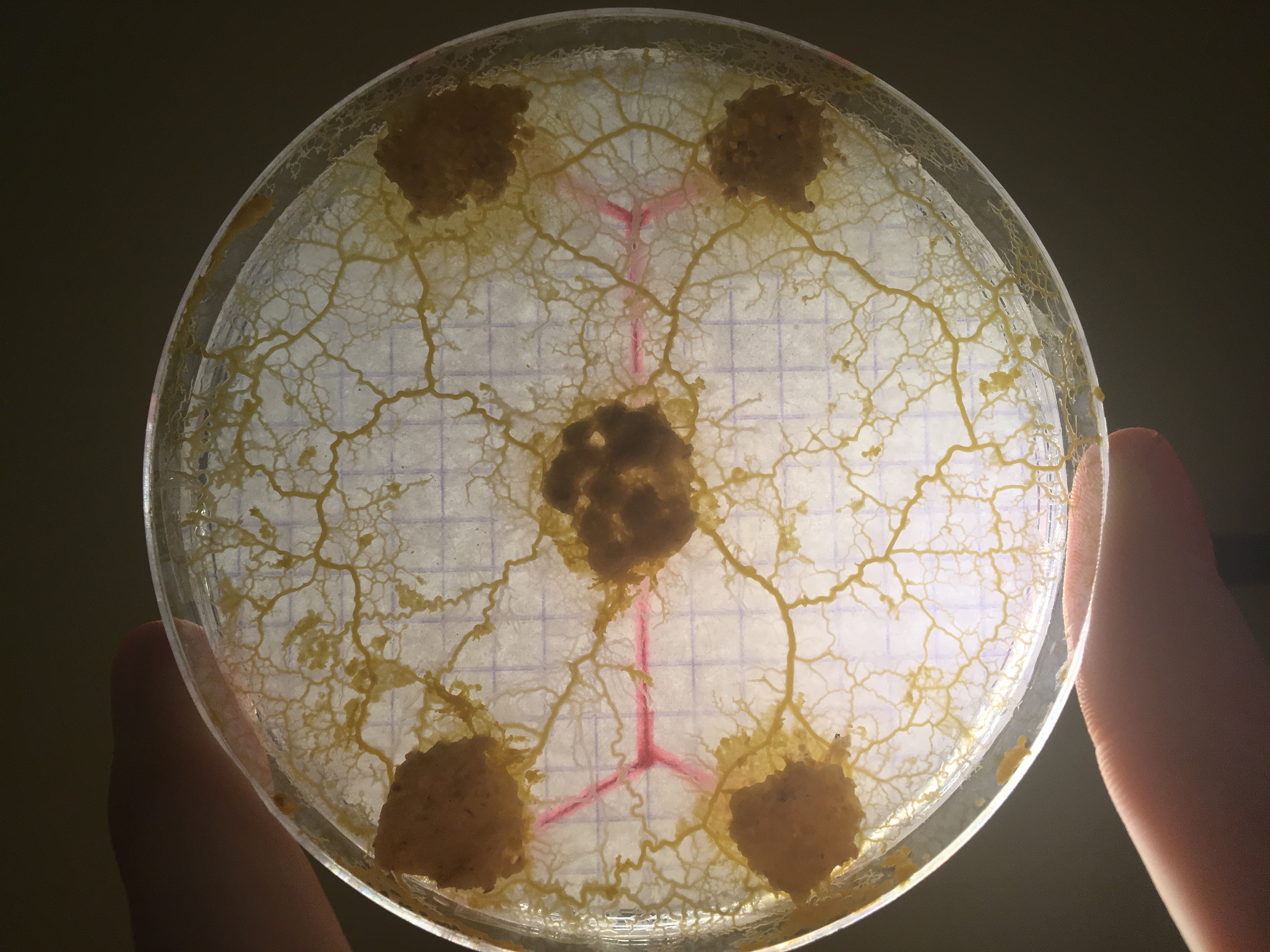
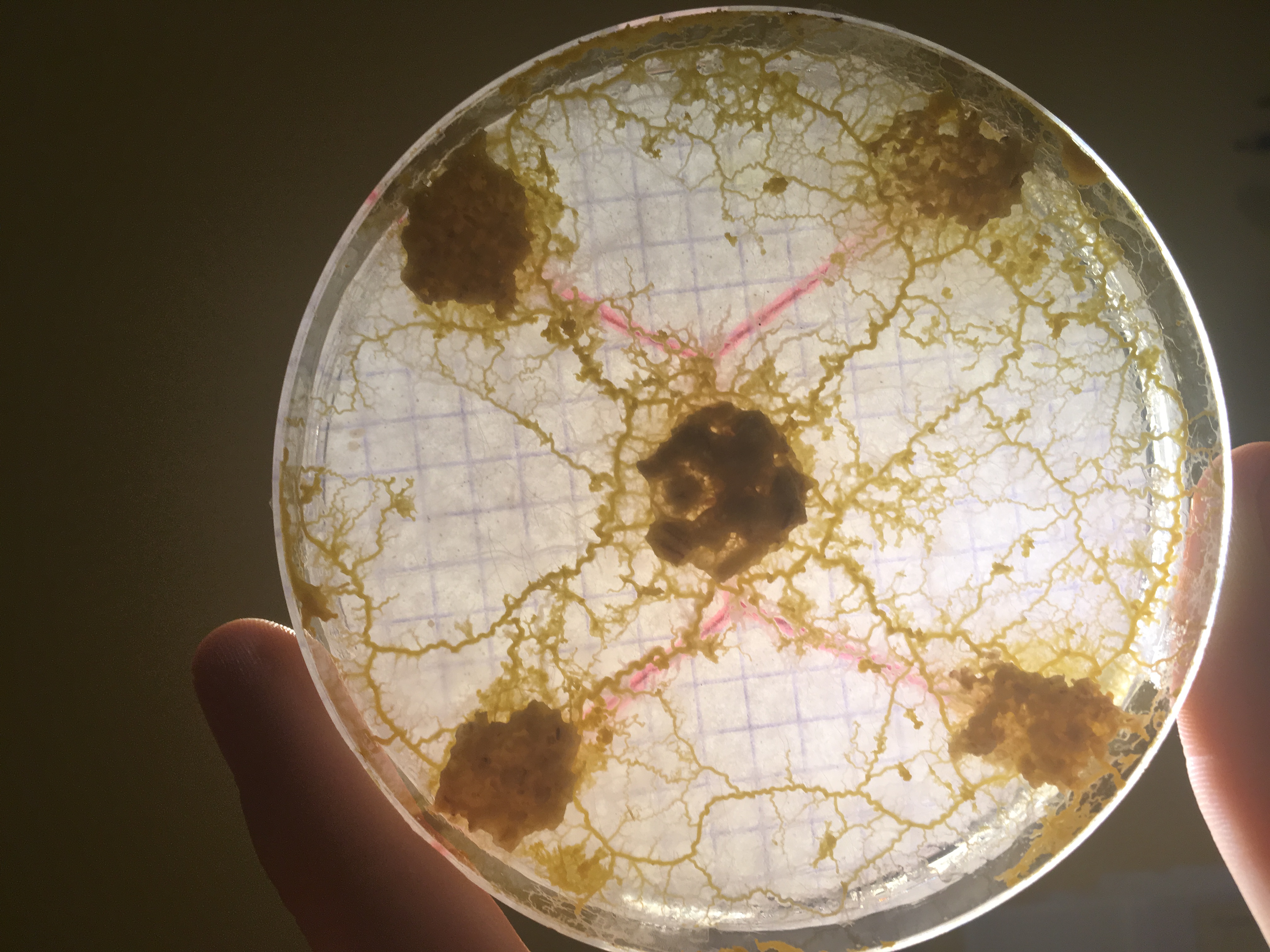
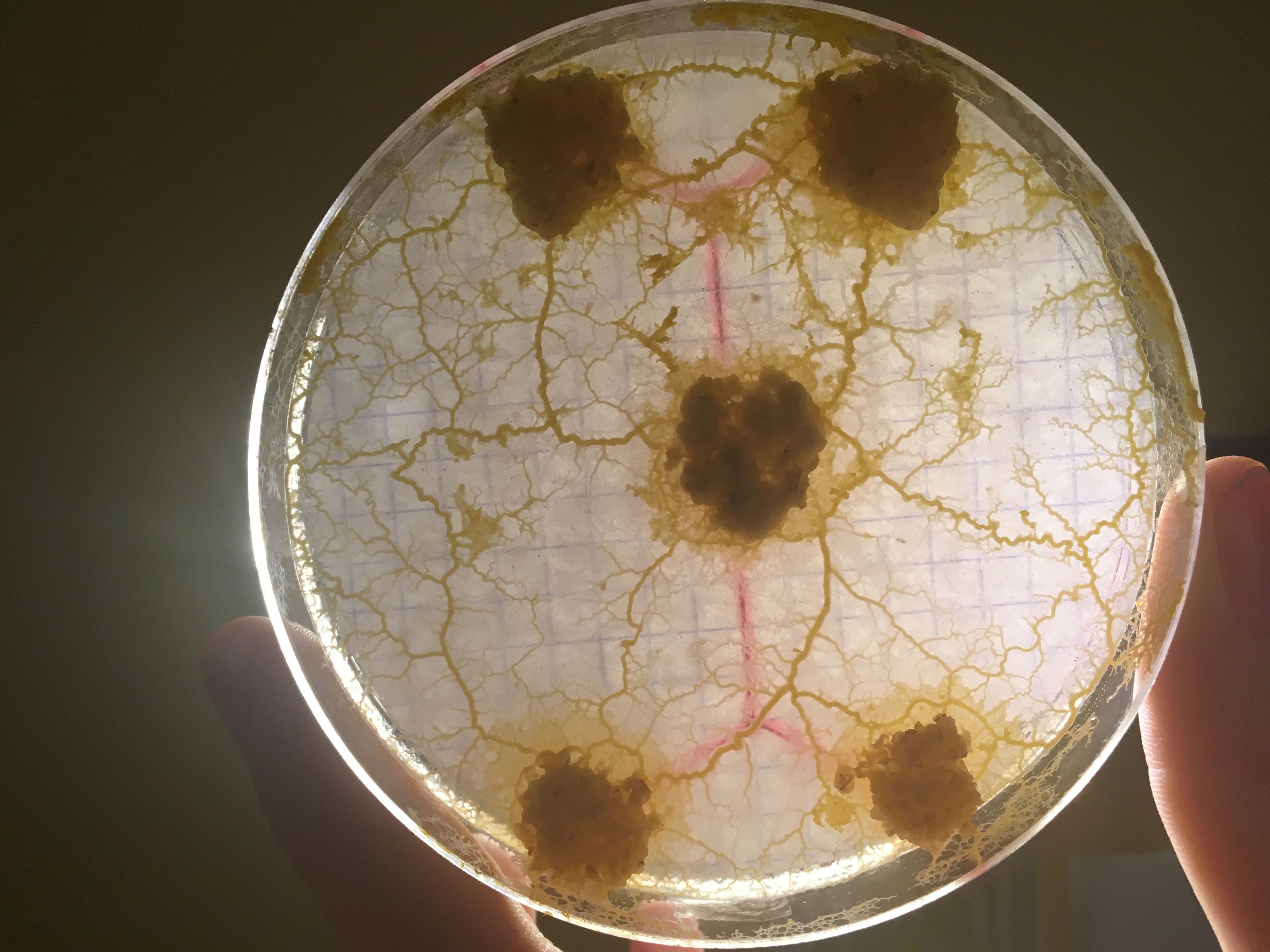
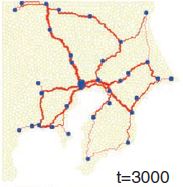
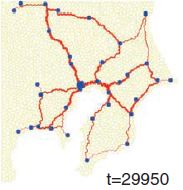
Des chercheurs japonais présentent un modèle mathématique de formation de réseau inspiré de la biologie du blob que l’on étudiera et que l’on cherchera à simuler. Le principe de ce modèle est que partant d’un espace couvert de blob, des canaux se forment qui ont tendance à croître ou à décroître selon leur utilité pour transporter la nourriture. Le système évolue et lorsqu’il s’arrête, il atteint une structure presque optimale du point de vue de l’énergie dépensée et de la robustesse à des modifications suites à des dommages causés au blob.
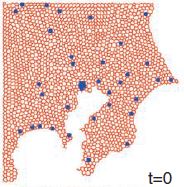
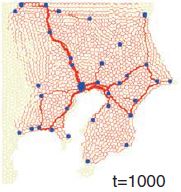
il est fort possible que le réseau formé par le blob ne soit pas optimal au point de vue de la distance totale, mais qu’il ait de meilleures propriétés de robustesse ou de distance moyenne entre les noeuds que la solution du problème de Steiner. Ce sont des propriétés également intéressantes pour un réseau de voies ferrées, on voudrait certes construire le minimum de voies, mais aussi éviter que certaines zones deviennent inaccessibles si une ligne tombe en panne, ou bien minimiser le temps de parcours des passagers, autant de paramètres qui pourraient pousser à privilégier un autre réseau que la solution au problème de Steiner. En s’inspirant de la biologie du blob, Tero et al. ont proposé un modèle calculable qui reproduit des réseaux semblables à ceux formés par le blob et par le réseaux des voies ferrées de Tokyo:
- L’espace est discrétisé, c’est à dire qu’il est représenté par des points discrets voisins les uns des autre,
- On part de l’état où le blob a recouvert tout l’espace disponible, et il existe des canaux qui lient entre eux les points voisins dans l’espace,
- Chaque source de nourriture, placée sur des points de l’espace, pompe des nutriments tantot dans l’organisme du blob, tantot hors de l’organisme du blob,
- En chaque point de l’espace il y a une pression, liée à la quantité de nutriments présente en cet endroit,
- Entre points voisins, il s’échange des nutriments avec un flux qui dépend des pressions respectives et du diamètre du canal entre les voisin,
- Le diamètre des canaux évolue en fonction de leur utilité pour tranporter les nutriments entre les différentes sources,
- Après un certain temps, seuls subsistent les canaux importants, qui forment un réseau liant toutes les sources entre elles.