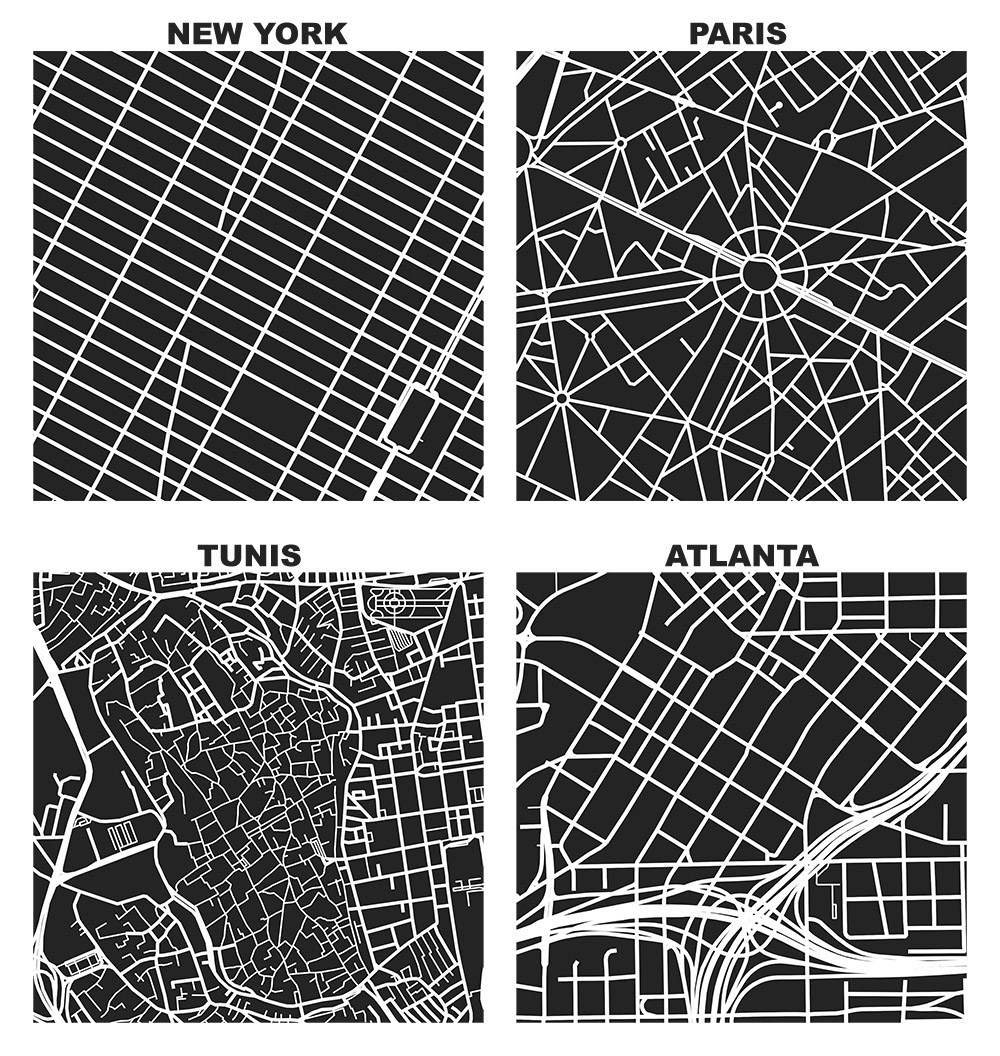
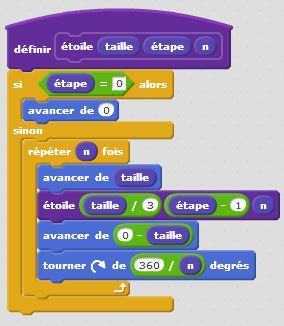
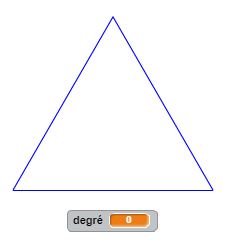
Des rues de Rome à celles de Paris en passant par celles de New York, nous nous rendons facilement compte que les axes de communication dessinent eux aussi des motifs géométriques particuliers. Ces axes de communication méritent notre attention : après avoir étudié l’organisation de leur contour, regardons à la loupe le découpage de la surface de nos villes et essayons de les modéliser à l’aide de motifs fractals. Le premier d’entre eux sera du type flocon. A partir du nombre de branches, nous calculons l’angle au centre qui les sépare. L’astuce réside ensuite dans le fait d’avancer, de reculer et de tourner de cet angle. La construction récursive du programme permet d’atteindre le degré fractal souhaité. Voilà ce que ça donne.
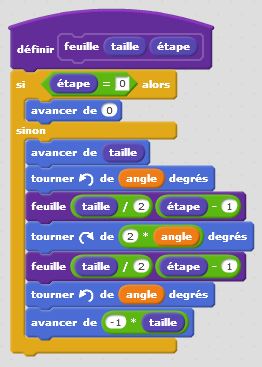
Après le flocon étudions les branches d’arbre. L’idée est la suivante : une branche se divise en deux formant un angle donné. J’avance, tourne de la moitié de l’angle, avance et recule, tourne de l’angle, avance et recule, tourne de la moitié de l’angle et recule pour revenir au point de départ. La construction récursive du programme permet de répéter ce même processus plusieurs fois à des échelles différentes. Voilà le résultat.
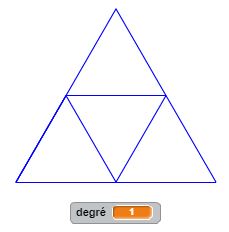
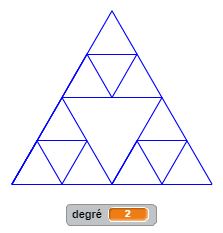
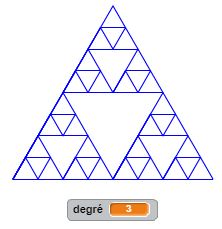
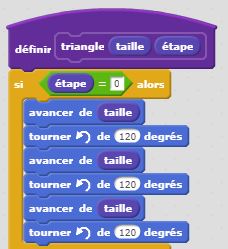
Pour varier les motifs, examinons comment est construit le triangle de Sierpinski : il est le résultat d’un processus itératif : partant d’un triangle, on le partage en quatre triangles en joignant les milieux de chaque côté, on supprime le triangle central et il nous reste trois triangles. Dans chacun des trois triangles restants on réitère l’opération et on supprime systématiquement le triangle central. Et ainsi de suite… La construction récursive de ce programme est un peu plus articulée mais permet d’obtenir des résultats probants. A vous de juger.
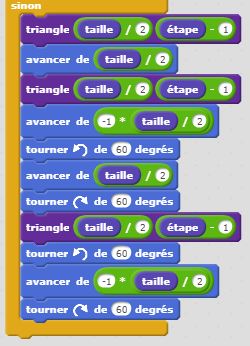
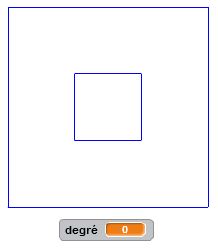
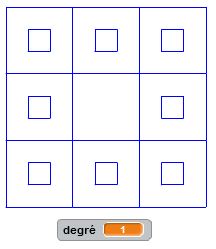
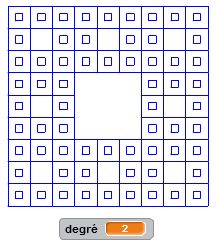
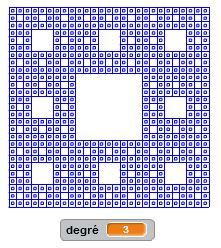
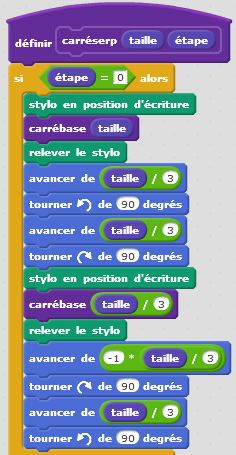
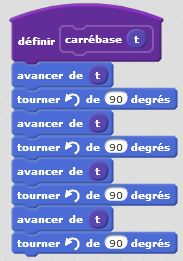
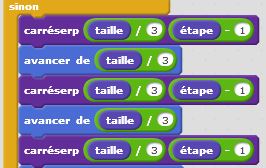
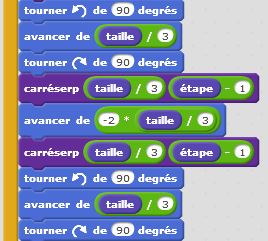
Le carré de Sierpinski est une fractale similaire au triangle de Sierpinski. Les triangles faisant place aux carrés. Le motif initial, qui sera répété plusieurs fois, est composé d’un carré de côté « c » dans lequel on enlève une partie centrale qui est un carré de côté « c/3 ». On supprime le carré central et on réitère le processus dans les huit carrés restants. Et ainsi de suite… La construction récursive de ce programme est toujours plus articulée mais permet d’obtenir des résultats très intéressants. Là encore, c’est à vous de juger.